Τι είναι ο Συντελεστής Συσχέτισης;
Ο συντελεστής συσχέτισης χρησιμοποιείται για να προσδιοριστεί πόσο ισχυρή είναι η σχέση μεταξύ δύο μεταβλητών και οι τιμές της μπορεί να κυμαίνονται από -1.0 έως 1.0, όπου -1.0 αντιπροσωπεύει αρνητική συσχέτιση και +1.0 αντιπροσωπεύει θετική σχέση. Λαμβάνει υπόψη τις σχετικές κινήσεις των μεταβλητών και στη συνέχεια καθορίζει εάν υπάρχει σχέση μεταξύ τους.
Τύπος συντελεστή συσχέτισης
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Που
- r = συντελεστής συσχέτισης
- n = αριθμός παρατηρήσεων
- x = 1 st μεταβλητή στο πλαίσιο
- y = 2 nd μεταβλητή
Εξήγηση
Εάν υπάρχει οποιαδήποτε συσχέτιση ή λέμε τη σχέση μεταξύ δύο μεταβλητών, τότε θα υποδεικνύει εάν μία από τις μεταβλητές αλλάζει στην τιμή, τότε η άλλη μεταβλητή θα τείνει επίσης να αλλάζει στην τιμή, ας πούμε συγκεκριμένα που θα μπορούσε να είναι είτε στην ίδια είτε στην την αντίθετη κατεύθυνση. Το μέρος του αριθμητή της εξίσωσης διεξάγει μια δοκιμή και τη σχετική ισχύ των μεταβλητών που κινούνται μαζί, και το μέρος του παρονομαστή της εξίσωσης κλιμακώνει τον αριθμητή πολλαπλασιάζοντας τις διαφορές των μεταβλητών από τις τετραγωνικές μεταβλητές.
Παραδείγματα
Παράδειγμα # 1
Εξετάστε τις ακόλουθες δύο μεταβλητές, x και y, πρέπει να υπολογίσετε τον συντελεστή συσχέτισης.
Παρακάτω δίνονται δεδομένα για τον υπολογισμό.

Λύση:
Χρησιμοποιώντας την παραπάνω εξίσωση, μπορούμε να υπολογίσουμε τα ακόλουθα

Έχουμε όλες τις τιμές στον παραπάνω πίνακα με n = 4.
Ας εισάγουμε τώρα τις τιμές για τον υπολογισμό του συντελεστή συσχέτισης.

Επομένως, ο υπολογισμός έχει ως εξής,

r = (4 * 25,032,24) - (262,55 * 317,31) / √ ((4 * 20,855,74) - (262,55) 2 ) * ((4 * 30,058,55) - (317,31) 2 )
r = 16,820,21 / 16,831,57
Ο συντελεστής θα είναι -

Συντελεστής = 0,99932640
Παράδειγμα # 2
Η Χώρα Χ είναι μια χώρα με αναπτυσσόμενη οικονομία και θέλει να πραγματοποιήσει μια ανεξάρτητη ανάλυση των αποφάσεων που έλαβε η κεντρική τράπεζά της σχετικά με τις μεταβολές των επιτοκίων, εάν αυτές έχουν επηρεάσει τον πληθωρισμό και έχουν τη δυνατότητα της κεντρικής τράπεζας να ελέγξει το ίδιο.
Ακολουθεί η σύνοψη του επιτοκίου και του πληθωρισμού που επικρατούσε στη χώρα κατά μέσο όρο για τα έτη αυτά.
Παρακάτω δίνονται δεδομένα για τον υπολογισμό.

Ο Πρόεδρος της χώρας σας πλησίασε για να πραγματοποιήσετε ανάλυση και να παρουσιάσετε την ίδια παρουσίαση στην επόμενη συνάντηση. Χρησιμοποιήστε τη συσχέτιση και καθορίστε εάν η κεντρική τράπεζα έχει εκπληρώσει τον στόχο της ή όχι.
Λύση:
Χρησιμοποιώντας τον τύπο που συζητήθηκε παραπάνω, μπορούμε να υπολογίσουμε τον συντελεστή συσχέτισης. Αντιμετώπιση του επιτοκίου ως μία μεταβλητή, ας πούμε x και αντιμετώπιση του επιτοκίου ως άλλης μεταβλητής ως y.

Έχουμε όλες τις τιμές στον παραπάνω πίνακα με n = 6.
Ας εισάγουμε τώρα τις τιμές για τον υπολογισμό του συντελεστή συσχέτισης.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Ο συσχετισμός θα είναι -

Συσχέτιση = -0,92
Ανάλυση: Φαίνεται ότι η συσχέτιση μεταξύ του επιτοκίου και του πληθωρισμού είναι αρνητική, η οποία φαίνεται να είναι η σωστή σχέση. Καθώς το επιτόκιο αυξάνεται, ο πληθωρισμός μειώνεται, πράγμα που σημαίνει ότι τείνουν να κινούνται προς την αντίθετη κατεύθυνση ο ένας από τον άλλο, και από το παραπάνω αποτέλεσμα φαίνεται ότι η κεντρική τράπεζα ήταν επιτυχής στην εφαρμογή της απόφασης σχετικά με την πολιτική επιτοκίων.
Παράδειγμα # 3
Το εργαστήριο ABC διεξάγει έρευνα σχετικά με το ύψος και την ηλικία και ήθελε να μάθει εάν υπάρχει σχέση μεταξύ τους. Έχουν συγκεντρώσει ένα δείγμα 1000 ατόμων για καθεμία από τις κατηγορίες και κατέληξαν σε ένα μέσο ύψος σε αυτήν την ομάδα.
Παρακάτω δίνονται δεδομένα για τον υπολογισμό του συντελεστή συσχέτισης.

Πρέπει να υπολογίσετε τον συντελεστή συσχέτισης και να καταλήξετε στο συμπέρασμα ότι εάν υπάρχει σχέση.
Λύση:
Αντιμετωπίζοντας την ηλικία ως μία μεταβλητή, ας πούμε x, και αντιμετωπίζοντας το ύψος (σε cms) ως μια άλλη μεταβλητή ως y.

Έχουμε όλες τις τιμές στον παραπάνω πίνακα με n = 6.
Ας εισάγουμε τώρα τις τιμές για τον υπολογισμό του συντελεστή συσχέτισης.

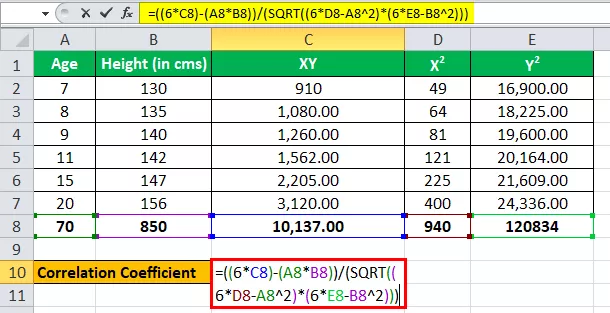
r = (6 * 10,137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1,322,00 / 1,361,23
Ο συσχετισμός θα είναι -

Συσχέτιση = 0,971177099
Συνάφεια και χρήση
Χρησιμοποιείται στις στατιστικές κυρίως για να αναλύσει την ισχύ της σχέσης μεταξύ των υπό εξέταση μεταβλητών και επιπλέον μετρά επίσης εάν υπάρχει γραμμική σχέση μεταξύ των δεδομένων συνόλων δεδομένων και πόσο καλά θα μπορούσαν να σχετίζονται. Ένα από τα κοινά μέτρα που χρησιμοποιούνται σε συσχετισμό είναι ο συντελεστής συσχέτισης Pearson.
Εάν μια μεταβλητή μεταβάλλει την τιμή και μαζί με άλλες μεταβλητές στην αξία, τότε η κατανόηση αυτής της σχέσης είναι κρίσιμη καθώς μπορεί κανείς να χρησιμοποιήσει την τιμή της προηγούμενης μεταβλητής για να προβλέψει την αλλαγή στην τιμή της τελευταίας μεταβλητής. Ένας συσχετισμός έχει πολλές πολλαπλές χρήσεις σήμερα σε αυτήν τη σύγχρονη εποχή, όπως χρησιμοποιείται στη χρηματοοικονομική βιομηχανία, στην επιστημονική έρευνα και όπου όχι. Ωστόσο, είναι σημαντικό να γνωρίζουμε ότι η συσχέτιση έχει τρεις βασικούς τύπους σχέσεων. Η πρώτη είναι μια θετική σχέση, η οποία δηλώνει εάν υπάρχει αλλαγή στην τιμή μιας μεταβλητής, τότε θα υπάρξει μια αλλαγή στη σχετική μεταβλητή προς την ίδια κατεύθυνση. Ομοίως, εάν υπάρχει αρνητική σχέση, τότε η σχετική μεταβλητή θα συμπεριφέρεται στην αντίθετη κατεύθυνση. Επίσης, εάν δεν υπάρχει συσχέτιση, τότε το r σημαίνει μηδενική τιμή.Δείτε τις παρακάτω εικόνες για να κατανοήσετε καλύτερα την έννοια.









