Τι είναι η τροποποιημένη διάρκεια;
Η τροποποιημένη διάρκεια λέει στον επενδυτή πόσο θα αλλάξει η τιμή του ομολόγου, δεδομένης της αλλαγής στην απόδοσή του. Καθώς ο κόσμος των ομολόγων είναι πιο περίπλοκος από τον κόσμο των μετοχών, είναι σημαντικό για τον επενδυτή να γνωρίζει την τροποποιημένη διάρκεια του ομολόγου. Για να υπολογίσει απλώς την τροποποιημένη διάρκεια του ομολόγου πρώτα, ο επενδυτής πρέπει να υπολογίσει ένα ακόμη πράγμα, που είναι η διάρκεια του Macauley. Για να υπολογίσει τη διάρκεια του Macauley, ο επενδυτής πρέπει να καταλάβει ποιος είναι ο χρόνος των ταμειακών ροών
Τύπος τροποποιημένης διάρκειας
Έτσι, ο τύπος για τροποποιημένη διάρκεια είναι απλά.
Τροποποιημένη διάρκεια = Διάρκεια Maculay / (1 + YTM / n)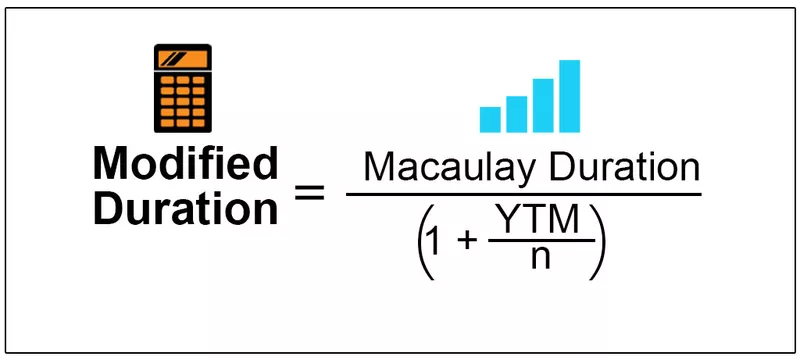
Που,
- Διάρκεια Macauley = Η διάρκεια υπολογίζει τον σταθμισμένο μέσο χρόνο πριν από τη λήψη των ταμειακών ροών του ομολόγου. Η τροποποιημένη διάρκεια διατάσσεται να υπολογίζεται πρώτα. Ο επενδυτής πρέπει να υπολογίσει τη διάρκεια του ομολόγου Macauley
- YTM = Απόδοση έως τη λήξη είναι απλώς η συνολική απόδοση που ο επενδυτής θα κέρδιζε σε ένα ομόλογο όταν το ομόλογο κρατήθηκε έως τη λήξη
- N = αριθμός περιόδων κουπονιών ανά έτος
Υπολογισμός τροποποιημένης διάρκειας με παραδείγματα
Παράδειγμα # 1
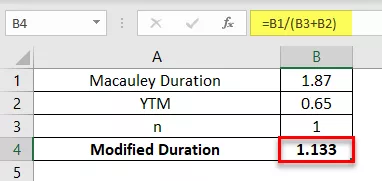
Μια διετής ετήσια πληρωμή ομολόγου 5.000 $ έχει διάρκεια Macaulay 1,87 χρόνια. Το YTM του ομολόγου είναι 6,5%. Υπολογίστε την τροποποιημένη διάρκεια του ομολόγου.
Παράδειγμα # 2
Μια διετής ετήσια πληρωμή ομολόγου 2.000 $ έχει διάρκεια Macaulay 2 ετών. Το YTM του ομολόγου είναι 5%. Υπολογίστε την τροποποιημένη διάρκεια του ομολόγου.

Παράδειγμα # 3
Μια τετραετής ετήσια πληρωμή ομολόγου 12.000 $ έχει διάρκεια Macaulay 5,87 χρόνια. Το YTM του ομολόγου είναι 4,5%. Υπολογίστε την τροποποιημένη διάρκεια του ομολόγου.

Παράδειγμα # 4
Μια 5ετής ετήσια πληρωμή 11.000 $ ομολόγων έχει διάρκεια Macaulay 1,5 χρόνια. Το YTM του ομολόγου είναι 7%. Υπολογίστε την τροποποιημένη διάρκεια του ομολόγου.

Πλεονεκτήματα
- Το κύριο πλεονέκτημα είναι ότι ο επενδυτής πρέπει να γνωρίζει τη διάρκεια του ομολόγου, καθώς η μεταβλητότητα των τιμών των ομολόγων σχετίζεται άμεσα με τις τιμές των ομολόγων. Όσο μεγαλύτερη είναι η διάρκεια του ομολόγου, τόσο μεγαλύτερη είναι η μεταβλητότητα των τιμών
- Η διάρκεια οποιουδήποτε επενδυτικού μέσου μπορεί να βοηθήσει στη διαχείριση καλύτερων επενδυτικών αναγκών για το μέλλον καθώς ο επενδυτής μπορεί να σχεδιάσει αποτελεσματικά τη μελλοντική πορεία της επένδυσής του στη διάρκεια
- Είναι επίσης ένα μέτρο του κινδύνου του ομολόγου για τη μεταβολή και της απόδοσης στην τιμή του ομολόγου
- Η μέση διάρκεια του αμοιβαίου κεφαλαίου είναι επίσης σημαντική, διότι σας λέει πόσο ευαίσθητο θα είναι το αμοιβαίο κεφάλαιο στις αλλαγές στα επιτόκια της αγοράς
Μειονεκτήματα
- Ο υπολογισμός τροποποιημένης διάρκειας είναι πολύπλοκος λόγω του υπολογισμού της διάρκειας του Macaulay και, στη συνέχεια, ο χρήστης ή ο επενδυτής χρειάζεται επίσης τις εισροές απόδοσης και τη διάρκεια του υπολογισμού της τροποποιημένης διάρκειας
- Η λήψη ακριβών εισροών και επικρατούν στην αγορά είναι δύσκολο να επιτευχθεί καθώς οι διακυμάνσεις των τιμών και οι τιμές της αγοράς αλλάζουν κάθε λεπτό, γεγονός που καθιστά τον υπολογισμό λανθασμένο και ξεπερασμένο
- Η διάρκεια δεν είναι επίσης ένα πλήρες μέτρο του κινδύνου που περιέχει η τιμή του ομολόγου και η διάρκεια του ομολόγου. Ο επενδυτής δεν μπορεί να αναμετάσχει αποκλειστικά στο μέτρο διάρκειας για να παράγει ακριβή μέτρα κινδύνου
- Η διάρκεια του Macaulay υπολογίζει τη σταθμισμένη μέση διάρκεια του ομολόγου, η οποία δεν είναι κάθε φορά καλό μέτρο του κινδύνου στο ομόλογο
συμπέρασμα
Τροποποιημένο και Macaulay παρόλο που οι περιορισμοί είναι πράγματι μια πολύ χρήσιμη ιδέα, ειδικά για τους διαχειριστές χαρτοφυλακίου για τη μέτρηση της μεταβλητότητας του ομολόγου και του κινδύνου που σχετίζεται με αυτό, ως εκ τούτου μπορεί να χρησιμεύσει ως ένα πολύ χρήσιμο εργαλείο όταν ο διαχειριστής δημιουργεί ένα χαρτοφυλάκιο ομολόγων και τη διαχείριση του κινδύνου που σχετίζεται με αυτό.








