Τύπος για τον υπολογισμό της πληρωμής προσόδων
Ο όρος «πρόσοδος» αναφέρεται στη σειρά των περιοδικών πληρωμών που θα λαμβάνονται είτε στην αρχή κάθε περιόδου είτε στο τέλος της περιόδου στο μέλλον. Ο τύπος για την πληρωμή προσόδων και το οφειλόμενο ποσό προσόδου υπολογίζεται με βάση το ΦΒ ενός οφειλόμενου προσόδου, πραγματικού επιτοκίου και ορισμένων περιόδων.
Ο τύπος που βασίζεται σε ένα συνηθισμένο πρόσοδο υπολογίζεται με βάση το PV ενός συνηθισμένου προσόδου, το πραγματικό επιτόκιο και αρκετές περιόδους.
Πρόσοδος = r * PVA συνηθισμένο / (1 - (1 + r) -n )που,
- PVA Ordinary = Τρέχουσα τιμή ενός συνηθισμένου προσόδου
- r = Πραγματικό επιτόκιο
- n = Αριθμός περιόδων
Μαθηματικά, η εξίσωση για οφειλόμενη πρόσοδος παρουσιάζεται ως,
Προσοχή = r * PVA Προθεσμία / ((1 - (1 + r) -n ) * (1 + r))που,
- PVA Due = Τρέχουσα τιμή οφειλόμενου προσόδου
- r = Πραγματικό επιτόκιο
- n = αριθμός περιόδων

Πώς να υπολογίσετε την πληρωμή προσόδων; (Βήμα βήμα)
Ο υπολογισμός της πληρωμής προσόδου μπορεί να προκύψει χρησιμοποιώντας το PV της συνηθισμένης προσόδου στα ακόλουθα βήματα:
- Βήμα 1 : Πρώτον, προσδιορίστε το PV της προσόδου και επιβεβαιώστε ότι η πληρωμή θα πραγματοποιηθεί στο τέλος κάθε περιόδου. Συμβολίζεται με PVA Ordinary .
- Βήμα 2: Στη συνέχεια, καθορίστε το επιτόκιο με βάση την τρέχουσα απόδοση της αγοράς. Στη συνέχεια, το πραγματικό επιτόκιο υπολογίζεται διαιρώντας το ετήσιο επιτόκιο με τον αριθμό των περιοδικών πληρωμών σε ένα έτος, και δηλώνεται με r. r = Ετήσιο επιτόκιο / Αριθμός τακτικών πληρωμών σε ένα έτος
- Βήμα 3: Στη συνέχεια, καθορίστε τον αριθμό των περιόδων πολλαπλασιάζοντας τον αριθμό των περιοδικών πληρωμών σε ένα έτος και τον αριθμό των ετών, και δηλώνεται με n. n = αριθμός τακτικών πληρωμών σε ένα έτος * Αριθμός ετών
- Βήμα 4: Τέλος, η πληρωμή προσόδου βάσει ΦΒ μιας συνηθισμένης προσόδου υπολογίζεται με βάση τη ΦΒ μιας συνηθισμένης προσόδου (βήμα 1), το πραγματικό επιτόκιο (βήμα 2) και ορισμένες περιόδους (βήμα 3), όπως φαίνεται παραπάνω.
Ο υπολογισμός της πληρωμής προσόδου μπορεί επίσης να προκύψει με τη χρήση της φωτοβολταϊκής περιόδου που οφείλεται στα ακόλουθα βήματα:
- Βήμα 1: Αρχικά, προσδιορίστε το PV της προσόδου και επιβεβαιώστε ότι η πληρωμή θα πραγματοποιηθεί στην αρχή κάθε περιόδου. Συμβολίζεται με PVA Due .
- Βήμα 2: Στη συνέχεια, καθορίστε το επιτόκιο με βάση την τρέχουσα απόδοση της αγοράς. Στη συνέχεια, το πραγματικό επιτόκιο υπολογίζεται διαιρώντας το ετήσιο επιτόκιο με τον αριθμό των περιοδικών πληρωμών σε ένα έτος, και δηλώνεται με r. r = Ετήσιο επιτόκιο / Αριθμός τακτικών πληρωμών σε ένα έτος
- Βήμα 3: Στη συνέχεια, καθορίστε τον αριθμό των περιόδων πολλαπλασιάζοντας τον αριθμό των περιοδικών πληρωμών σε ένα έτος και τον αριθμό των ετών, και δηλώνεται με n. n = αριθμός τακτικών πληρωμών σε ένα έτος * Αριθμός ετών
- Βήμα 4: Τέλος, η πληρωμή προσόδου βάσει ΦΒ ενός οφειλόμενου προσόδου υπολογίζεται με βάση το ΦΒ ενός οφειλόμενου προσόδου (βήμα 1), το πραγματικό επιτόκιο (βήμα 2) και αρκετές περιόδους (βήμα 3), όπως φαίνεται παραπάνω.
Παραδείγματα
Παράδειγμα # 1
Ας πάρουμε το παράδειγμα του David, ο οποίος κέρδισε λαχειοφόρο αγορά αξίας 10.000.000 $. Έχει επιλέξει μια πληρωμή προσόδου στο τέλος κάθε έτους για τα επόμενα 20 χρόνια ως επιλογή πληρωμής. Καθορίστε το ποσό που θα καταβάλει ο David ως πληρωμή προσόδου εάν το σταθερό επιτόκιο στην αγορά είναι 5%.
Παρακάτω δίνονται τα δεδομένα που χρησιμοποιούνται για τον υπολογισμό των πληρωμών προσόδου.
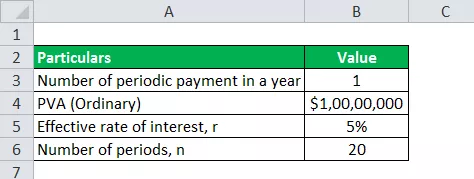
PVA Ordinary = 10.000.000 $ (από το ποσό που πληρώνεται στο τέλος κάθε έτους)
Επομένως, ο υπολογισμός της πληρωμής προσόδου μπορεί να γίνει ως εξής -
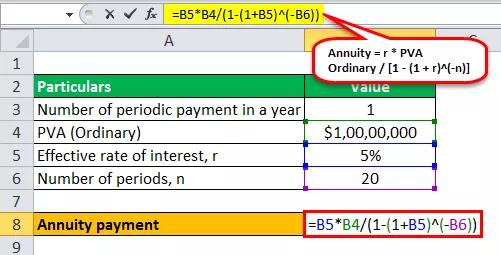
- Πρόσοδος = 5% * 10.000.000 $ / (1 - (1 + 5%) -20 )
Ο υπολογισμός της Πληρωμής Προσόδου θα είναι -

- Ετήσια = 802.425,87 $ ~ 802,426 $
Επομένως, ο David θα πληρώσει πληρωμές προσόδου 802.426 $ για τα επόμενα 20 χρόνια σε περίπτωση συνηθισμένης προσόδου.
Παράδειγμα # 2
Ας πάρουμε το παραπάνω παράδειγμα του Δαβίδ και να καθορίσουμε την πληρωμή προσόδου αν πληρώνεται στην αρχή κάθε έτους με όλες τις άλλες προϋποθέσεις ίδιες.
Θα χρησιμοποιήσουμε τα ίδια δεδομένα με το παραπάνω παράδειγμα για τον υπολογισμό των πληρωμών προσόδων.
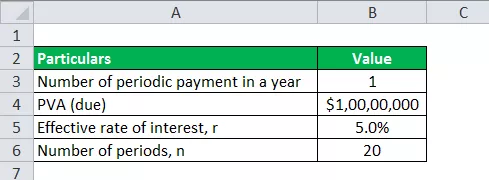
Επομένως, ο υπολογισμός της πληρωμής προσόδου μπορεί να γίνει ως εξής -
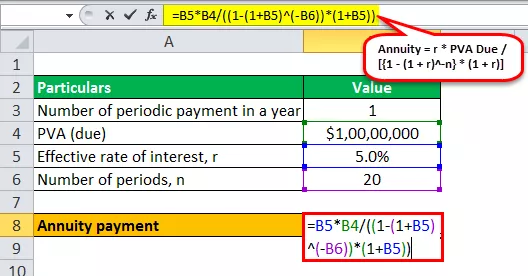
- Προσοχή = r * PVA Προθεσμία / ((1 - (1 + r) -n ) * (1 + r))
- Πρόσοδος = 5% * 10.000.000 $ / ((1 - (1 + 5%) -20 ) * (1 + 5%))
Ο υπολογισμός της Πληρωμής Προσόδου θα είναι -
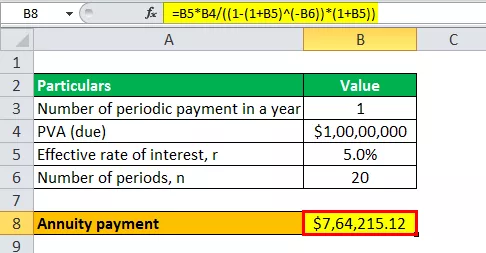
- Ετήσια = 764,215,12 $ ~ 764,215 $
Ως εκ τούτου, ο David θα πληρώσει πληρωμές προσόδου 764.215 $ για τα επόμενα 20 χρόνια σε περίπτωση οφειλόμενης προσόδου.
Υπολογιστής προσόδων
Μπορείτε να χρησιμοποιήσετε την ακόλουθη αριθμομηχανή προσόδων.
| Συνηθισμένο PVA | |
| ρ | |
| ν | |
| Τύπος προσόδων = | |
| Τύπος προσόδων = | r * |
|
||||||||
| 0 * |
|
Συνάφεια και χρήσεις
Η πληρωμή προσόδου είναι μία από τις εφαρμογές της χρονικής αξίας του χρήματος, η οποία υποδεικνύεται περαιτέρω από τη διαφορά μεταξύ των πληρωμών προσόδου βάσει των συνήθων προσόδων και των οφειλόμενων προσόδων. Η χαμηλότερη πληρωμή προσόδου για μια πρόσοδο είναι ότι τα χρήματα λαμβάνονται στην αρχή κάθε περιόδου. Πιστεύεται ότι τα κεφάλαια θα επενδυθούν στην αγορά και οι τόκοι θα κερδίσουν κατά τη διάρκεια αυτής της περιόδου.
Η εξίσωση για την πληρωμή προσόδων βρίσκει εφαρμογή στον υπολογισμό των προσόδων εισοδήματος, των αποσβεσμένων δανείων, των πληρωμών λαχειοφόρων αγορών, των δομημένων διακανονισμών και οποιουδήποτε άλλου τύπου σταθερών περιοδικών πληρωμών.








