Ποια είναι η παρούσα αξία της διαιώνιας;
Η διαιώνιση μπορεί να οριστεί ως η ροή εισοδήματος που λαμβάνει το άτομο για άπειρη χρονική περίοδο και η παρούσα αξία του επιτυγχάνεται με προεξόφληση των ίδιων ταμειακών ροών με το προεξοφλητικό επιτόκιο. Εδώ οι ταμειακές ροές είναι άπειρες αλλά η παρούσα αξία της ανέρχεται σε περιορισμένη αξία.
Εξήγηση
Το Perpetuity είναι μια σειρά ταμειακών ροών που έχουν άπειρη ζωή και μια τέτοια ροή εισοδήματος αυξάνεται με αναλογικό επιτόκιο. Οι ταμειακές ροές πρέπει να είναι ίδιες.
Ο τύπος βασικά προέρχεται από το μοντέλο ανάπτυξης μερισμάτων. Ο τύπος επιχειρεί να προσδιορίσει την τελική αξία των ίδιων ταμειακών ροών. Επομένως, η παρούσα αξία των ταμειακών ροών στη βασική έκφραση μπορεί να προκύψει ως εξής:
Τρέχουσα τιμή = D / (1 + r) + D x (1 + g) / (1 + r) 2 + D / (1 + r) + D x (1 + g) 2 / (1 + r) 3….
Τρέχουσα τιμή = D / r

Τρέχουσα αξία του τύπου Αιώνια
Ο τύπος εκφράζεται ως εξής: -
PV of Perpetuity = ICF / rΕδώ,
- Οι ίδιες ταμειακές ροές θεωρούνται ως CF.
- Το επιτόκιο ή το προεξοφλητικό επιτόκιο εκφράζεται ως r.
Εάν η διαιώνιση αυξάνεται με σταθερό ρυθμό ανάπτυξης, τότε θα εκφραστεί όπως περιγράφεται παρακάτω:
PV of Perpetuity = ICF / (r - g)Εδώ,
- Οι ίδιες ταμειακές ροές θεωρούνται ως CF.
- Το επιτόκιο ή το προεξοφλητικό επιτόκιο εκφράζεται ως r.
- Ο ρυθμός ανάπτυξης εκφράζεται ως g.
Πώς να υπολογίσετε την παρούσα αξία της διαιώνιας;
Για να υπολογίσετε ότι έχει προεξοφλητικό επιτόκιο, πρέπει να εκτελούνται τα ακόλουθα βήματα όπως φαίνεται παρακάτω:
Βήμα 1 - Επιλέξτε το χρηματοοικονομικό μέσο ή το περιουσιακό στοιχείο που παρέχει βιώσιμες άπειρες ταμειακές ροές για ολόκληρο τον κύκλο ζωής του. Τέτοια χρηματοοικονομικά περιουσιακά στοιχεία ή μέσα θα μπορούσαν να είναι ενοικιαζόμενα ακίνητα, ενοικιαζόμενα εμπορικά ακίνητα, προτιμώμενα αποθέματα και ομόλογα.
Βήμα # 2 - Στη συνέχεια, Προσδιορίστε τις ίδιες ταμειακές ροές ή τη ροή εσόδων.
Βήμα # 3 - Στη συνέχεια, καθορίστε το προεξοφλητικό επιτόκιο.
Βήμα # 4 - Για να φτάσετε στο φωτοβολταϊκό της διαρκείας, διαιρέστε τις ταμειακές ροές με την προκύπτουσα τιμή που καθορίζεται στο βήμα 3.
Για τον υπολογισμό της φωτοβολταϊκής διαρκείας που έχει προεξοφλητικό ποσοστό και ρυθμό ανάπτυξης, πρέπει να εκτελούνται τα ακόλουθα βήματα όπως φαίνεται παρακάτω: -
Βήμα 1 - Επιλέξτε το χρηματοοικονομικό μέσο ή το περιουσιακό στοιχείο που παρέχει βιώσιμες άπειρες ταμειακές ροές για ολόκληρο τον κύκλο ζωής του. Τέτοια χρηματοοικονομικά περιουσιακά στοιχεία ή μέσα θα μπορούσαν να είναι ενοικιαζόμενα ακίνητα, ενοικιαζόμενα εμπορικά ακίνητα, προτιμώμενα αποθέματα και ομόλογα.
Βήμα # 2 - Στη συνέχεια, Προσδιορίστε τις ίδιες ταμειακές ροές ή τη ροή εσόδων.
Βήμα # 3 - Στη συνέχεια, καθορίστε το προεξοφλητικό επιτόκιο.
Βήμα # 4 - Στη συνέχεια, καθορίστε τον ρυθμό ανάπτυξης, εάν υπάρχει, που αντιστοιχεί στις άπειρες ταμειακές ροές.
Βήμα # 5 - Στη συνέχεια, προσδιορίστε τη διαφορά μεταξύ του προεξοφλητικού επιτοκίου και του ρυθμού ανάπτυξης.
Βήμα # 6 - Για να φτάσετε στην παρούσα αξία της διαρκούς διάρκειας, διαιρέστε τις ταμειακές ροές με την προκύπτουσα τιμή που καθορίζεται στο βήμα 5.
Παραδείγματα
Παράδειγμα # 1
Ας πάρουμε λοιπόν το παράδειγμα μιας εμπορικής επιχείρησης. Η επιχείρηση σκοπεύει να λάβει εισόδημα 120.000 $ για άπειρη θητεία. Το κόστος κεφαλαίου για την επιχείρηση είναι στο 13 τοις εκατό. Οι ταμειακές ροές αυξάνονται σε αναλογική βάση 3 τοις εκατό. Βοηθήστε τη διοίκηση να το προσδιορίσει.
Λύση
Υπολογισμός Φ / Β Αέναιας
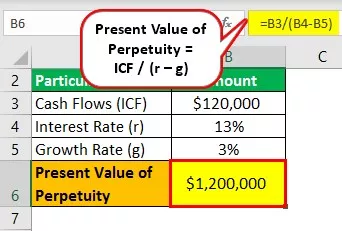
- = 120 $ 000 / (13% - 3%)
- = 1.200.000 $
Παράδειγμα # 2
Ας πάρουμε λοιπόν το παράδειγμα ενός μεμονωμένου επενδυτή που κατέχει προτιμητέες μετοχές στην εταιρεία ABC. Η επιχείρηση σκοπεύει να διανείμει προτιμώμενα μερίσματα 20 $ ανά μετοχή για άπειρη θητεία. Το απαιτούμενο ποσοστό απόδοσης για τον επενδυτή είναι 8%. Οι ταμειακές ροές αυξάνονται σε αναλογική βάση 2 τοις εκατό. Ο επενδυτής κατέχει σήμερα 200 μετοχές της εταιρείας ABC. Βοηθήστε τον επενδυτή να το καθορίσει. Υπολογίστε τη συνολική αξία των μερισμάτων όπως φαίνεται παρακάτω: -
Λύση
Συνολική αξία μερισμάτων

Η συνολική αξία μερισμάτων = Προνομιακό μέρισμα ανά μετοχή x αριθμός μετοχών
- = $ 20 x 200
- Συνολική αξία μερισμάτων = 4.000 $
Υπολογισμός Φ / Β Αέναιας

- = 4 $ 000 / (8% - 2%)
- = 66.666,67 $
Παράδειγμα # 3
Ας πάρουμε λοιπόν το παράδειγμα του συστήματος χρηματοδότησης. Το πρόγραμμα σκοπεύει να παρέχει εισόδημα 320.000 $ για άπειρη θητεία. Το απαιτούμενο ποσοστό απόδοσης είναι 10 τοις εκατό. Βοηθήστε τον επενδυτή να το καθορίσει;
Λύση
Υπολογισμός της Τρέχουσας Αξίας της Διαιώνιας

- = 320 $, 000/10%
- = 3.200.000 $
Χρήσεις
- Η διαιώνιση χρησιμοποιείται συνήθως σε προτιμώμενα αποθέματα.
- Οι προτιμώμενες μετοχές τείνουν να παρέχουν σταθερά μερίσματα καθ 'όλη τη διάρκεια του κύκλου ζωής της εταιρείας.
- Δεδομένου ότι η διαιώνιση είναι ένα άπειρο ποσό, η παρούσα αξία του βοηθά στην επίτευξη μιας αξίας που έχει περιορισμένο ποσό.
- Η διαιώνιση έχει τις εφαρμογές της και στην ακίνητη περιουσία.
- Εάν το ακίνητο παρέχει μια ροή βιώσιμου εισοδήματος, τότε η παρούσα αξία της προκύπτει χρησιμοποιώντας τη σχέση της παρούσας αξίας μιας διαιώνιας.
- Επιπρόσθετα, το φωτοβολταϊκό της διαρκούς διαμόρφωσης αποτελεί τη βάση για πολλά προγράμματα προικοδότησης και προγραμματισμό συνταξιοδότησης.
- Τα συστήματα χρηματοδότησης είναι προγράμματα χρηματοοικονομικής προστασίας που παρέχουν χρηματοοικονομική προστασία καθώς και ένα ολοκληρωμένο σχέδιο αποταμίευσης.
- Τέτοια συστήματα, εάν σχεδιαστούν σωστά, μπορούν να προσφέρουν μια σταθερή ροή εισοδήματος για άπειρη θητεία.
συμπέρασμα
Η διαιώνιση είναι πανομοιότυπες ταμειακές ροές που λαμβάνονται για άπειρη θητεία. Το PV αυτών των ροών εισοδήματος προκύπτει διαιρώντας με προεξοφλητικό επιτόκιο και ορίζεται ως η παρούσα αξία μιας διαιώνιας. Η διαιώνιση που καθορίζεται μέσω του προεξοφλητικού επιτοκίου μπορεί να ποικίλει εάν ο χρηματοοικονομικός αναλυτής τροποποιήσει το προεξοφλητικό επιτόκιο σε περιοδικά επίπεδα.








