Υπολογιστής απλών αποταμιεύσεων - Υπολογίστε το ποσό ωριμότητας του ατόμου

Σχετικά με τον Υπολογιστή Απλών Αποταμιεύσεων

Ο τύπος έχει ως εξής:

Μαθηματικά μπορεί να υπολογιστεί για εφάπαξ εξοικονόμηση:

Δεύτερον, εάν πραγματοποιούνται μηνιαίες απλές αποταμιεύσεις, ο υπολογισμός:

Εν,

• M είναι το συνολικό ποσό στο τέλος της απλής περιόδου εξοικονόμησης
• Είμαι το αρχικό ποσό που επενδύεται
• είναι το σταθερό ποσό που επενδύεται σε τακτά χρονικά διαστήματα
• r είναι το επιτόκιο
• F είναι η συχνότητα των τόκων που πληρώνονται
• n είναι ο αριθμός των περιόδων για τις οποίες θα γίνει απλή εξοικονόμηση.

Υπάρχουν πολλές τράπεζες και άλλα χρηματοπιστωτικά ιδρύματα που ανταγωνίζονται στην αγορά για να προσελκύσουν καταθέσεις, ώστε να μπορούν να κάνουν περισσότερες επιχειρήσεις, δηλαδή, δανεισμός χρημάτων σε εταιρείες ή άτομα με καθαρή αξία. Ορισμένες τράπεζες θα πληρώνουν υψηλότερο επιτόκιο εάν οι καταθέσεις υπερβαίνουν ορισμένα όρια και διατηρούνται στον λογαριασμό, αλλιώς, θα πληρώσουν ένα τυπικό επιτόκιο. Επιπλέον, μπορεί να υπάρχει διαφορά στις συχνότητες της πληρωμής τόκου. Για παράδειγμα, οι τόκοι θα μπορούσαν να επιδεινωθούν και να καταβληθούν ανά τρίμηνο, εξαμηνιαία ή ετησίως ανάλογα με την τράπεζα. Επομένως, με αυτόν τον υπολογιστή, τα άτομα θα μπορούσαν να καθορίσουν ποιο χρηματοοικονομικό ίδρυμα θα πρέπει να επιλέξουν να επενδύσουν τα χρήματά τους συγκρίνοντας το ποσό λήξης ή την απόδοση που κερδίζουν στα κύρια ποσά τους.

Πώς να υπολογίσετε τις απλές αποταμιεύσεις;

Κάποιος πρέπει να ακολουθήσει τα παρακάτω βήματα για να υπολογίσει την απλή εξοικονόμηση.

Βήμα # 1 - Προσδιορίστε ποιο ποσό θα επενδυθεί, είτε πρόκειται για εφάπαξ είτε υπάρχει και περιοδική επένδυση, τότε το ίδιο θα πρέπει να ληφθεί υπόψη για σύγκριση υπολογισμών ποσοστών εξοικονόμησης.

Βήμα # 2 - Υπολογίστε το επιτόκιο που είναι διαθέσιμο στις επιλογές για το άτομο, και το οποίο θα κερδίσει ή αναμένεται να κερδίσει με την απλή αποταμίευση.

Βήμα # 3 - Τώρα, καθορίστε την περίοδο για την οποία θα επενδυθεί, και κυρίως αυτές θα είναι μακροπρόθεσμα και θα εξαρτώνται κατά περίπτωση.

Βήμα # 4 - Διαιρέστε το επιτόκιο με τον αριθμό περιόδων που καταβάλλεται ο τόκος ή ο τόκος απλής αποταμίευσης. Για παράδειγμα, εάν το καταβληθέν επιτόκιο είναι 5% και πληρώνει μηνιαία, τότε το επιτόκιο θα είναι 5% / 12, δηλαδή 0,416%.

Βήμα # 5- Τώρα χρησιμοποιήστε τον τύπο που συζητήθηκε παραπάνω στο σημείο 1) σε περίπτωση που το Simple Savings γίνεται κατ 'αποκοπή και χρησιμοποιήστε τον τύπο 2) σε περίπτωση που το ποσό Simple Savings γίνεται σε τακτά χρονικά διαστήματα μαζί με οποιοδήποτε αρχικό ποσό για όλες τις διαθέσιμες επιλογές .

Βήμα # 6 - Το προκύπτον ποσό θα είναι το ποσό λήξης που θα περιλαμβάνει και το εισόδημα Simple Savings και επέλεξε αυτό που έχει την υψηλότερη πληρωμή από άποψη τόκων.

Παράδειγμα απλής αποταμίευσης υπολογισμού

Ο κ. William είναι πλέον ενήλικας και είναι ενθουσιασμένος που ανοίγει τον πρώτο του λογαριασμό ταμιευτηρίου. Έψαξε για το χρηματοπιστωτικό ίδρυμα, το οποίο παρέχει υψηλό επιτόκιο, αλλά είναι μπερδεμένος καθώς δεν παίρνει γιατί η τράπεζα θα του προσφέρει την υψηλότερη απόδοση. Ακολουθούν τα αποσπάσματα που έχει επιλέξει ο κ. Γουίλιαμ.

Θέλει να επενδύσει 1.500 $ σε έναν από τους λογαριασμούς και θα επενδύσει με τον τρόπο που ο λογαριασμός πληρώνει τόκους. Για παράδειγμα, εάν η τράπεζα πληρώνει εξαμηνιαία, τότε το ποσό θα επενδυθεί εξίσου στο τέλος κάθε περιόδου και θα συνεχίσει να το κάνει για περίοδο 10 ετών.

Με βάση τις δεδομένες πληροφορίες, πρέπει να υπολογίσετε το ποσό στο οποίο θα εξοικονομούσε, και τους τόκους που θα κερδίσει για το ίδιο, και σε ποια Τράπεζα θα πρέπει να επιλέξει να επενδύσει.

Λύση:

Μας δίνονται οι παρακάτω λεπτομέρειες:

ΤΡΑΠΕΖΑ I

• I = Το αρχικό ποσό θα είναι μηδέν
• r = Επιτόκιο που είναι 3,00% και Τριμηνιαίο θα είναι 3,00% / 4 που είναι 0,75%
• N = Συχνότητα που είναι τριμηνιαία εδώ. ως εκ τούτου θα είναι 4
• n = αριθμός ετών που πρέπει να γίνουν οι Απλές Αποταμιεύσεις, δηλαδή 10 χρόνια εδώ.
• i = Το κανονικό ποσό που πρόκειται να επενδυθεί, το οποίο είναι 1500/4 που είναι 375 $

Τώρα, μπορούμε να χρησιμοποιήσουμε τον παρακάτω τύπο για να υπολογίσουμε το ποσό λήξης.

• = 0 * (1 + 0,75%) ^{10 * 4} + 375 * ((1 + 0,75%) ^{10 * 4} - 1 / 0,75%)
• = 17,417,43

Το ποσό λήξης θα είναι 17.417,43

Οι συνδυασμένοι τόκοι που θα αποκτηθούν θα είναι 17,417,43 $ - $ (375 * 40) = 2.417,43 $

ΤΡΑΠΕΖΑ II

• I = Το αρχικό ποσό θα είναι μηδέν
• r = Επιτόκιο που είναι 3,12% και Εξαμηνιαίο θα είναι 3,12% / 2 που είναι 1,56%.
• N = Συχνότητα που είναι εξαμηνιαία εδώ, επομένως θα είναι 2
• n = αριθμός ετών που πρέπει να γίνουν οι Απλές Αποταμιεύσεις, δηλαδή 10 χρόνια εδώ.
• i = Το κανονικό ποσό που πρόκειται να επενδυθεί, το οποίο είναι 1500/2 που είναι 750 $

Τώρα, μπορούμε να χρησιμοποιήσουμε τον παρακάτω τύπο για να υπολογίσουμε το ποσό λήξης.

• = 0 * (1 + 1,56%) ^{10 * 2} + 750 * ((1 + 1,56%) ^{10 * 2} - 1) / 1,56%
• = 17.445,58 $

Η τιμή λήξης θα είναι 17.445,58 $

Ο συνδυασμένος τόκος που θα αποκτηθεί θα είναι 17.445,58 $ - (750 $ * 20) = 2.445,58 $.

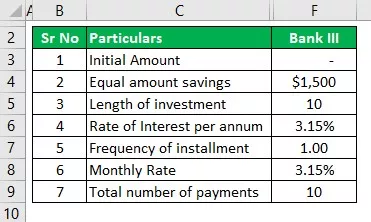
ΤΡΑΠΕΖΑ III

• I = Το αρχικό ποσό θα είναι μηδέν
• r = Επιτόκιο, που είναι 3,15%, και ετησίως θα είναι 3,15% / 1, που είναι 3,15%
• N = Συχνότητα που είναι Ετησίως εδώ, άρα θα είναι 1
• n = αριθμός ετών που πρέπει να γίνουν οι Απλές Αποταμιεύσεις, δηλαδή 10 χρόνια εδώ.
• i = Είναι το κανονικό ποσό που πρόκειται να επενδυθεί, το οποίο είναι 1500/1 που είναι 1.500 $

Τώρα, μπορούμε να χρησιμοποιήσουμε τον παρακάτω τύπο για να υπολογίσουμε το ποσό λήξης.

• = 0 * (1 + 3,15%) ^{10 * 1} + 1500 * ((1 + 3,15%) ^{10 * 1} - 1) / 3,15%
• = 17,315,08 $

Το ποσό λήξης θα είναι 17.315,08 $

Οι συνδυασμένοι τόκοι που κερδίστηκαν θα ήταν 17.315,08 $ - (1500 $ 10) = 2.315,08 $.

Το υψηλότερο κέρδος είναι στην Τράπεζα II, και ως εκ τούτου θα πρέπει να ανοίξει λογαριασμό στην Τράπεζα II.

συμπέρασμα

Αυτός ο υπολογιστής, όπως συζητήθηκε παραπάνω, μπορεί να χρησιμοποιηθεί για να συγκρίνει τα διαφορετικά ποσά λήξης στο χρηματοπιστωτικό ίδρυμα, καθώς ένα υψηλότερο επιτόκιο δεν εγγυάται το υψηλότερο απόλυτο ποσό, όπως φαίνεται στο παραπάνω παράδειγμα. Ως εκ τούτου, πρέπει κανείς να υπολογίσει και να συγκρίνει τα ποσά κατά τη λήξη και στη συνέχεια να λάβει απόφαση.