Υπολογιστής αποπληρωμής χρέους - Υπολογίστε τη διάρκεια μετά την αποπληρωμή του χρέους

Υπολογιστής αποπληρωμής χρεών

Ο υπολογιστής αποπληρωμής χρέους είναι ένας τύπος αριθμομηχανής όπου, εάν ο οφειλέτης επιθυμεί να ενοποιήσει τα εκκρεμή δάνεια και να προσπαθήσει να τα εξοφλήσει γρήγορα για να μειώσει την επιβάρυνση τόκων και το πλεόνασμα εκροής.

Σχετικά με τον Υπολογιστή Αποπληρωμής Χρέους

Κατ 'αρχάς, μάθετε την παρούσα αξία των υπολοίπων των πολλαπλών δανείων

Στη συνέχεια θα ήταν να ανακαλύψετε το νέο ποσό δόσης, το οποίο θα μπορούσε να είναι είτε το άθροισμα του υπάρχοντος ποσού δόσης και επιπλέον πληρωμή, εάν υπάρχει.

Τώρα υπολογίστε την περίοδο εντός της οποίας μπορεί να εξοφληθεί το χρέος

Εν,

• Η PV είναι η παρούσα αξία του Υπόλοιπο
• Το L είναι η υπάρχουσα πληρωμή
• Το L 'είναι η νέα πληρωμή
• είναι το επιτόκιο
• n είναι η συχνότητα των πληρωμών
• nPVA είναι ο αριθμός των περιοδικών πληρωμών

Είναι ένας εύχρηστος υπολογιστής, καθώς θα υπολογίσει ποια θα είναι η θητεία όταν εξοφλούνται όλα τα χρέη. Σε αυτήν την περίπτωση, ο οφειλέτης μπορεί να κάθεται με πολλαπλά δάνεια με διαφορετικά επιτόκια και είναι πρόθυμος να τα ενοποιήσει. Περαιτέρω, ο οφειλέτης θα μπορούσε ακόμη και να επιθυμεί να αυξάνει περιοδικά το ποσό δόσης ή να ενοποιεί επίσης το ποσό δόσης. Αυτό θα τον βοηθήσει να μειώσει την επιβάρυνση των τόκων και επίσης να εκκαθαρίσει το χρέος νωρίς. Η απόφαση δεν είναι τόσο εύκολη όσο απαιτείται για την αύξηση του ποσού δόσης, κάτι που θα μπορούσε να αυξήσει την επιβάρυνση της ταμειακής ροής του δανειολήπτη. Αυτός ο υπολογιστής θα βοηθήσει μόνο στον υπολογισμό εντός του χρονικού διαστήματος που μπορούν να εξοφλήσουν πλήρως το χρέος όταν ενοποιούνται τα χρέη.

Πώς να υπολογίσετε χρησιμοποιώντας τον υπολογιστή αποπληρωμής χρέους;

Κάποιος πρέπει να ακολουθήσει τα παρακάτω βήματα για να υπολογίσει τη διάρκεια του ενοποιημένου χρέους.

Βήμα # 1 - Πρώτον, ο οφειλέτης πρέπει να καθορίσει ποιο είναι το τρέχον υπόλοιπο του χρέους που δεν είναι παρά να ανακαλύψει την παρούσα αξία του Χρέους.

Βήμα 2 - Τώρα καθορίστε το νέο ποσό δόσης, το οποίο είναι το άθροισμα του υπάρχοντος ποσού δόσης που πληρώνει επί του παρόντος και το επιπλέον ποσό με το οποίο ο οφειλέτης σκέφτεται να ξεκινήσει.

Βήμα # 3 - Μάθετε το δάνειο, το οποίο έχει υψηλότερο επιτόκιο και καταστήστε σαφές ότι το χρέος εξοφλείται πρώτα και συνεχίζει να πληρώνει ελάχιστο ή ποσό δόσης για άλλα εκκρεμή δάνεια.

Βήμα # 4 - Τώρα υπολογίστε το οφειλόμενο κεφάλαιο για τα υπόλοιπα δάνεια και υπολογίστε τη διάρκεια του δανείου με το νέο ποσό δόσης.

Βήμα # 5 - Η προκύπτουσα θητεία μπορεί να μετατραπεί σε χρόνια διαιρώντας την τιμή που έφτασε στο βήμα 4 με 12 και οι αριθμοί στη δεξιά πλευρά του δεκαδικού μπορούν να πολλαπλασιαστούν επί 12 για να τους πάρουν σε μήνες.

Παράδειγμα

Ο κ. Χ έχει δύο δάνεια σε εκκρεμότητα, ένα είναι αυτόματο δάνειο και ένα άλλο είναι ενυπόθηκο δάνειο.

Οι λεπτομέρειες και των δύο δανείων δίνονται παρακάτω:

Ο διευθυντής υποκαταστήματος πλησίασε τον κ. X με ένα σχέδιο στο οποίο μπορεί να ενοποιήσει τα τρέχοντα εκκρεμή δάνεια και να εξοφλήσει το χρέος νωρίς. Ο τραπεζίτης του παρείχε λεπτομέρειες σχετικά με το πρόγραμμα που επρόκειτο να εξοφλήσει το υψηλότερο χρέος πρώτα και στη συνέχεια να συνεχίσει το σταθερό ποσό του κλειστού δανείου που θα αποπληρωθεί στο ενυπόθηκο δάνειο που θα μειώσει τη διάρκεια του κλεισίματος του δανείου. Ο κ. X συμφώνησε επίσης να αυξήσει το ποσό της δόσης κατά 200 $ ενώ ενοποιώντας τα εκκρεμή δάνεια και θα συνεχίσει να το κάνει μέχρι να εξοφληθούν τα χρέη.

Πρέπει να υπολογίσετε τη διάρκεια με την οποία θα εξοφληθεί το χρέος.

Λύση:

Πρέπει να υπολογίσουμε την παρούσα αξία του τρέχοντος οφειλόμενου υπολοίπου, το οποίο μπορεί να υπολογιστεί σύμφωνα με τον παρακάτω τύπο:

Αυτόματο δάνειο

Επιτόκιο που εφαρμόζεται σε μηνιαία βάση = 8/12 = 0,67%

Η υπόλοιπη περίοδος θα είναι (7 * 12) - (3 * 12) που είναι 84 - 36, δηλαδή 48.

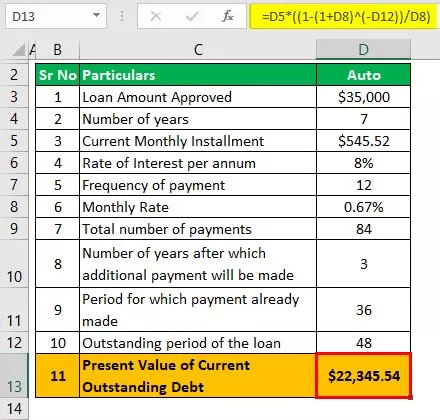
• = 545 $. 52 * (1 - (1 + 0,67%) ^-48 ) / 0,67%)
• = 22.345,54 $

Στεγαστικό δάνειο

Επιτόκιο που εφαρμόζεται σε μηνιαία βάση = 5/12 = 0,42%

Η υπόλοιπη περίοδος θα είναι (25 * 12) - (10 * 12) που είναι 300 - 120 που είναι 180.

• = 1,227,64 $ * (1 - (1 + 0,42%) ^-180 / 0,42%)
• = 155.241,51 $

Ενοποιημένο υπόλοιπο δανείου

• = 22.345,44 $ + 155.241,40 $
• = 177.586,84 $

Μας δίνεται εδώ, η υπάρχουσα μηνιαία δόση που πληρώνει για ένα αυτόματο δάνειο είναι 545,52 $ και το υπάρχον ποσό δόσης σε ένα στεγαστικό δάνειο είναι 1,227,64 $. Το ενοποιημένο ποσό δόσης θα ήταν 1.773,16 $ και επιπλέον ο κ. X θέλει επίσης να αυξήσει αυτό το ποσό κατά 200 $. Επομένως, το συνολικό ποσό της νέας δόσης θα είναι 1.973,16 $

Πρώτον, το ποσό δόσης του αυτόματου δανείου θα εξοφληθεί από το υψηλότερο επιτόκιο και το νέο ποσό που θα χρησιμοποιηθεί για την αποπληρωμή του αυτόματου δανείου θα ήταν 545,52 $ + 200 $ που είναι 745,52 $ και το υπόλοιπο θα χρησιμοποιηθεί για την πληρωμή Στεγαστικό δάνειο ύψους 1.973,16 $ - 745,52 $ που ισούται με 1,227,64 $

Τώρα, θα υπολογίσουμε σε ποιο χρονικό διάστημα θα εκκαθαριστεί το αυτόματο δάνειο

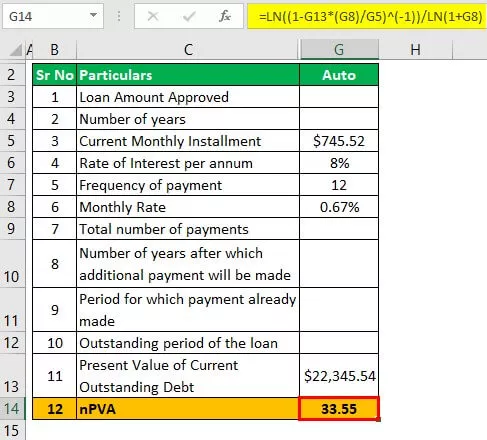
• = ln (((1- 22,345,44 * (0,67%) / 745,52) ^-1 ) / ln (1 + 0,67%)
• = 33.55

Τώρα η εκκρεμή διάρκεια του στεγαστικού δανείου θα ήταν 180 μείον 33,55 που είναι 146,45

Στεγαστικό δάνειο μετά την αποπληρωμή του αυτόματου δανείου

Επιτόκιο που εφαρμόζεται σε μηνιαία βάση = 5/12 = 0,42%

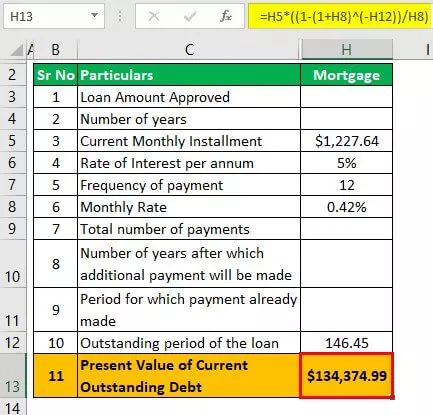
• = 1,227,64 $ * (1 - (1 + 0,42%) ^-146,45 / 0,42%)
• = 134.374,99 $

Τώρα, θα υπολογίσουμε σε ποιο χρονικό διάστημα θα εκκαθαριστεί το στεγαστικό δάνειο

• = ln (((1- 134.374,92 * (0,42%) / 1,973,16) ^-1 ) / ln (1 + 0,42%)
• = 80.26

Επομένως, η συνολική διάρκεια εντός της οποίας μπορεί να εκκαθαριστεί το δάνειο είναι 33,55 + 80,26, που είναι 113,81 και όταν διαιρείται το ίδιο με 12 που είναι 9,48 έτη που είναι σε 9 χρόνια και 6 μήνες.